Lagrangian approach to deriving the gravity equations in the new theory.

 Ruslan Sharipov

 1 ... 9 10 11 ... ru

The Lagrangian approach to deriving various equations is associated with the name of Joseph Louis Lagrange. Detailed information about him can be found in Wikipedia. In mechanics and in physics his name is associated with the so-called "least action principle". According to this principle, the evolution of a physical system occurs in such a way that some integral over time turns out to take the smallest possible value. This integral is called the action integral. It is usually denoted by the letter S.

The function L in the integral S is called the Lagrange function or the Lagrangian. In field theories it is itself an integral over spatial variables.
In the spatial integral L we see a function denoted by the same letter, but in a calligraphic style. This is the Lagrangian density. It is represented as the sum of two terms: the Lagrangian density of the gravitational field and the Lagrangian density of matter. We will discuss the Lagrangian density of the gravitational field  in a separate article. As for the Lagrangian density of matter, it depends on a specific type of matter. It can be cosmic dust, gas, liquid, solid, or even dark matter.
Applying the least action principle to the integral S leads to the Euler-Lagrange equations. In our case, they are divided into two groups of six equations and of one equation, respectively. The group of six equations is written as follows.
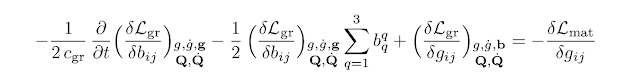
Here i ≤ j. The remarkable fact is that this group of six equations coincides with the six equations that were written out in the post "Einstein's equation and consequences from it in the new theory". These same six equations were discussed in the post "Discussion of the obtained gravity equations". The following equality follows from the coincidence of the equations obtained in two different ways.

The second group of Euler-Lagrange equations contains one single equation. It has the following form.

And again this Euler-Lagrange equation coincides with the only equation in the second group of gravity equations, which was considered in the post "Einstein's equation and consequences from it in the new theory" and discussed in the post "Discussion of the obtained gravity equations". From the coincidence of the gravity equations obtained in two different ways, the following equality follows.

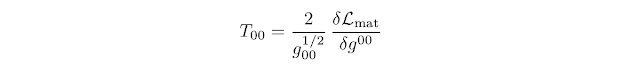
The obtained formulas allow us to calculate the components of the four-dimensional energy-momentum tensor while remaining within the framework of the three-dimensional formalism.



Comments

Post a Comment

Popular posts from this blog

Criticism of the space-time sausage

Image
  Criticism of the space-time sausage. Ruslan A. Sharipov 1 2 3 ... ru The concept of space-time arose in the early 20th century in connection with Einstein's theory of relativity. It is a combination of three-dimensional space and one-dimensional time, which had previously been considered separately, into one four-dimensional continuum. We cannot depict a four-dimensional continuum graphically. Therefore we reduce the three-dimensional space to the two-dimensional space and reserve the third dimension for to image the time. As a result we get the following picture. The horizontal planes on the picture symbolize the states of the universe at different instants in time during its evolution. In fact, they are three-dimensional and there are not two of them, but infinitely many. They fill the entire four-dimensional space-time. Instead of considering the entire universe, we can limit ourselves to some part of it. For example, the globe. Then we get the ...
Read more
Image
Discussion of the obtained gravity equations. Ruslan A. Sharipov.  1 ... 8 9 10 ... ru   We shall discuss the equations of the gravitational field in the new theory of gravity, which is called « 3D-brane universe model ». I am the author of this theory. Therefore, you will receive first-hand information without any distortion. The gravity equations in the new theory are subdivided into two groups. The equations of the first group have the form They depend on two indices i and j . When these indices are rearranged, the equations do not change. Therefore, different equations are obtained only for the following values of the indices: (i=1,j=1), (i=1,j=2), (i=1,j=3), (i=2,j=2), (i=2,j=3), (i=3,j=3). This means that the total number of different equations in the first group is 6. The second group of gravity equations in the new theory contains only one equation. As a result, the total number of the gravity equations in the ...
Read more
Image
Einstein's equation and consequences from it in the new theory. Ruslan A. Sharipov. 1 ... 7 8 9 ... ru   Einstein's equation was written by him in 1915. A historical essay about it can be found in Wikipedia . It captivated and captivates many people with its simplicity and elegance. In Wikipedia you will find this equation written with the plus sign in front of the constant Λ. I wrote it with the minus sign. This is my mistake. It was admitted long time ago in 1997, when I was writing my textbook “ Classical electrodynamics and  theory of relativity .” The Internet in Russia and in the city of Ufa was much less accessible that time than it is now. Also there was no Wikipedia; it appeared only in 2001. It was necessary to go to libraries and rummage through catalogs in search of even older textbooks. But I was lazy. In order not to contradict my textbook, I now write Einstein’s equation with the minus sign in front of Λ. This is not a big problem. It is enough to take the...
Read more