The field of normals and comoving coordinates

The field of normals and comoving coordinates.

Ruslan A. Sharipov

1 ...  4 5 6 ... ru  

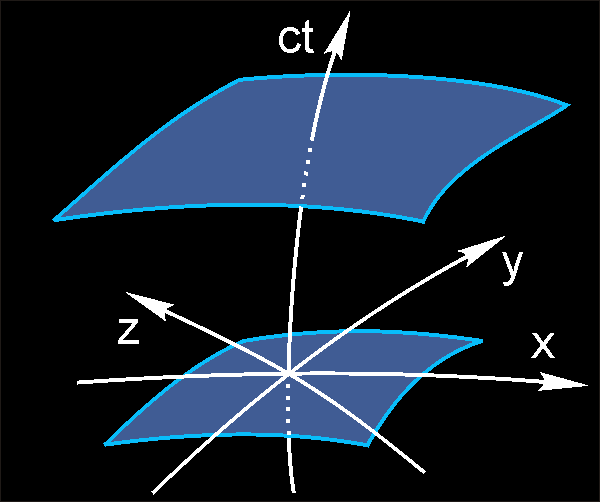
In the new theory, which is called the 3D-brane universe model, there is a special infinite family of 3D-branes (see 3D-branes in thespace-time). It turns spacetime into a 3D brane foliation. Each brane in this foliation corresponds to a specific instant in the evolution of the universe. Only one of the branes corresponds to the current instant, that is, the instant of the present. It is that very brane that has the prototype in the form of the real three-dimensional physical universe in its current state. The remaining branes correspond to past states of the universe that have ceased to exist, and its future states that have not yet formed.

Let us choose at each point of each 3D-brane the vector of unit length perpendicular to the brane and directed towards the future. Such vectors form the vector field of unit normal vectors to the branes.

 

Each vector field has integral curves. This is a mathematical fact. Integral curves of a vector field are curves whose tangent vectors at each point are directed along the vectors of the vector field. In our case the integral curves of the field of unit normal vectors to the branes fill the entire space-time and connect  to each other all of the branes from the 3D-brane foliation.

By choosing x, y, z coordinates on one of the 3D-branes, they can be extended to all other 3D-branes of the foliation along the integral lines of the unit normal vector field. The coordinates x, y, z throughout the space-time obtained in this way are called comoving coordinates. They are usually supplemented with a special fourth coordinate, which is called the brane time t.

Comments

Post a Comment

Popular posts from this blog

Criticism of the space-time sausage

Image
  Criticism of the space-time sausage. Ruslan A. Sharipov 1 2 3 ... ru The concept of space-time arose in the early 20th century in connection with Einstein's theory of relativity. It is a combination of three-dimensional space and one-dimensional time, which had previously been considered separately, into one four-dimensional continuum. We cannot depict a four-dimensional continuum graphically. Therefore we reduce the three-dimensional space to the two-dimensional space and reserve the third dimension for to image the time. As a result we get the following picture. The horizontal planes on the picture symbolize the states of the universe at different instants in time during its evolution. In fact, they are three-dimensional and there are not two of them, but infinitely many. They fill the entire four-dimensional space-time. Instead of considering the entire universe, we can limit ourselves to some part of it. For example, the globe. Then we get the ...
Read more
Image
Discussion of the obtained gravity equations. Ruslan A. Sharipov.  1 ... 8 9 10 ... ru   We shall discuss the equations of the gravitational field in the new theory of gravity, which is called « 3D-brane universe model ». I am the author of this theory. Therefore, you will receive first-hand information without any distortion. The gravity equations in the new theory are subdivided into two groups. The equations of the first group have the form They depend on two indices i and j . When these indices are rearranged, the equations do not change. Therefore, different equations are obtained only for the following values of the indices: (i=1,j=1), (i=1,j=2), (i=1,j=3), (i=2,j=2), (i=2,j=3), (i=3,j=3). This means that the total number of different equations in the first group is 6. The second group of gravity equations in the new theory contains only one equation. As a result, the total number of the gravity equations in the ...
Read more
Image
Einstein's equation and consequences from it in the new theory. Ruslan A. Sharipov. 1 ... 7 8 9 ... ru   Einstein's equation was written by him in 1915. A historical essay about it can be found in Wikipedia . It captivated and captivates many people with its simplicity and elegance. In Wikipedia you will find this equation written with the plus sign in front of the constant Λ. I wrote it with the minus sign. This is my mistake. It was admitted long time ago in 1997, when I was writing my textbook “ Classical electrodynamics and  theory of relativity .” The Internet in Russia and in the city of Ufa was much less accessible that time than it is now. Also there was no Wikipedia; it appeared only in 2001. It was necessary to go to libraries and rummage through catalogs in search of even older textbooks. But I was lazy. In order not to contradict my textbook, I now write Einstein’s equation with the minus sign in front of Λ. This is not a big problem. It is enough to take the...
Read more